Какая функция является производной. Правила вычисления производных

Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.

Правила дифференцирования

1. (k⋅ f(x))′=k⋅ f ′(x).
2. (f(x)+g(x))′=f′(x)+g′(x).
3. (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
4. Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
5. Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
6. Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
7. Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈ (a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
8. Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.

Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.

Содержание статьи

ПРОИЗВОДНАЯ –производной функции y = f (x ), заданной на некотором интервале (a , b ) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производную принято обозначать так:

Широко употребляются и другие обозначения:

Мгновенная скорость.

Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M 0 , зависит от времени t , т.е. s есть функция времени t : s = f (t ). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).

Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds . В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds .

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t . Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t . Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt . Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt , когда приращение времени стремится к нулю. Так как

Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления .

Пусть кривая есть график функции y = f (x ) в прямоугольной системе координат (см . рис.).

При некотором значении x функция имеет значение y = f (x ). Этим значениям x и y на кривой соответствует точка M 0(x , y ). Если аргументу x дать приращение Dx , то новому значению аргумента x + Dx соответствует новое значение функции y+ Dy = f (x + Dx ). Соответствующей ему точкой кривой будет точка M 1(x + Dx , y + Dy ). Если провести секущую M 0M 1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox , из рисунка непосредственно видно, что .

Если теперь Dx стремится к нулю, то точка M 1 перемещается вдоль кривой, приближаясь к точке M 0, и угол j изменяется с изменением Dx . При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M 0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:

Следовательно, f ´(x ) = tga

т.е. значение производной f ´(x ) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x ) в соответствующей точке M 0(x ,y ) с положительным направлением оси Ox .

Дифференцируемость функций.

Определение. Если функция y = f (x ) имеет производную в точке x = x 0, то функция дифференцируема в этой точке.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f (x ) непрерывна на отрезке [a ,b ], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f (a ) = f (b ) = 0), то внутри отрезка [a ,b ] существует, по крайней мере одна, точка x = с , a c b, в которой производная f ў(x ) обращается в нуль, т.е. f ў(c ) = 0.

Теорема о конечных приращениях (теорема Лагранжа). Если функция f (x ) непрерывна на отрезке [a , b ] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a , b ] найдется по крайней мере одна точка с , a c b, что

f (b ) – f (a ) = f ў(c )(b – a ).

Теорема об отношении приращений двух функций (теорема Коши). Если f (x ) и g (x ) – две функции, непрерывные на отрезке [a , b ] и дифференцируемые во всех внутренних точках этого отрезка, причем g ў(x ) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a , b ] найдется такая точка x = с , a c b, что

Производные различных порядков.

Пусть функция y = f (x ) дифференцируема на некотором отрезке [a , b ]. Значения производной f ў(x ), вообще говоря, зависят от x , т.е. производная f ў(x ) представляет собой тоже функцию от x . При дифференцировании этой функции получается так называемая вторая производная от функции f (x ), которая обозначается f ўў (x ).

Производной n- го порядка от функции f (x ) называется производная (первого порядка) от производной n- 1- го и обозначается символом y (n ) = (y (n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f (x ), где x – независимая переменная, есть dy = f ў(x )dx , некоторая функция от x , но от x может зависеть только первый сомножитель f ў(x ), второй же сомножитель (dx ) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x , то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2y :

d (dx ) = d 2y = f ўў(x )(dx ) 2 .

Дифференциалом n- го порядка называется первый дифференциал от дифференциала n- 1- го порядка:

d n y = d (d n –1 y ) = f (n )(x )dx (n ).

Частная производная.

Если функция зависит не от одного, а от нескольких аргументов x i (i изменяется от 1 до n , i = 1, 2,… n ), f (x 1, x 2,… x n ), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x i . Частная производная 1-ого порядка по x i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x i , сохраняют постоянные значения. Для частных производных вводятся обозначения

Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.

Анна Чугайнова

Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f"(x_0) \).

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f"(x_0) $$

Для обозначения производной часто используют символ y". Отметим, что y" = f(x) - это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .

Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f"(a) \)

Поскольку \(k = tg(a) \), то верно равенство \(f"(a) = tg(a) \) .

А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f"(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f"(x) \), т.е. \(\Delta y \approx f"(x) \cdot \Delta x \). Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х. Например, для функции \(y = x^2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) - f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f"(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f"(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f"(0) \)

Итак, мы познакомились с новым свойством функции - дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C - постоянное число и f=f(x), g=g(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования :

$$ C"=0 $$ $$ x"=1 $$ $$ (f+g)"=f"+g" $$ $$ (fg)"=f"g + fg" $$ $$ (Cf)"=Cf" $$ $$ \left(\frac{f}{g} \right) " = \frac{f"g-fg"}{g^2} $$ $$ \left(\frac{C}{g} \right) " = -\frac{Cg"}{g^2} $$ Производная сложной функции:
$$ f"_x(g(x)) = f"_g \cdot g"_x $$

Таблица производных некоторых функций

$$ \left(\frac{1}{x} \right) " = -\frac{1}{x^2} $$ $$ (\sqrt{x}) " = \frac{1}{2\sqrt{x}} $$ $$ \left(x^a \right) " = a x^{a-1} $$ $$ \left(a^x \right) " = a^x \cdot \ln a $$ $$ \left(e^x \right) " = e^x $$ $$ (\ln x)" = \frac{1}{x} $$ $$ (\log_a x)" = \frac{1}{x\ln a} $$ $$ (\sin x)" = \cos x $$ $$ (\cos x)" = -\sin x $$ $$ (\text{tg} x)" = \frac{1}{\cos^2 x} $$ $$ (\text{ctg} x)" = -\frac{1}{\sin^2 x} $$ $$ (\arcsin x)" = \frac{1}{\sqrt{1-x^2}} $$ $$ (\arccos x)" = \frac{-1}{\sqrt{1-x^2}} $$ $$ (\text{arctg} x)" = \frac{1}{1+x^2} $$ $$ (\text{arcctg} x)" = \frac{-1}{1+x^2} $$

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная - одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того - это нужно делать. При решении примеров по математике возьмите за правило - если можете упростить выражение, обязательно упрощайте .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Производная - главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x

Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Наиболее употребительны следующие обозначения производной :

Пример 1. Пользуясь определением производной , найти производную функции

Решение. Из определения производной вытекает следующая схема её вычисления.

Дадим аргументу приращение (дельта) и найдём приращение функции:

Найдём отношение приращения функции к приращению аргумента:

Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:

Физический смысл производной

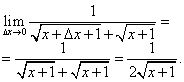
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле - задачи о мгновенной скорости неравномерного прямолинейного движения точки.

Пусть камешек поднят и затем из состояния покоя отпущен. Путь s , проходимый за время t , является функцией времени, то есть. s = s (t ). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени камешек находился в положении A , а в момент - в положении B . За промежуток времени (от t до ) точка прошла путь . Поэтому средняя скорость движения за этот промежуток времени, которую обзначим через , составляет

.

Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени . Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t ) называется предел средней скорости при :

(при условии, что этот предел существует и конечен).

Так выясняется, что мгновенная скорость есть предел отношения приращения функции s (t ) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.

.

Решение обозначенной задачи представляет собой физический смысл производной . Итак, производной функции y=f (x ) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Пример 2. Найти производную функции

Решение. Из определения производной вытекает следующая схема для её вычисления.

Шаг 1. Дадим аргументу приращение и найдём

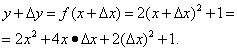
Шаг 2. Найдём приращение функции:

Шаг 3. Найдём отношение приращения функции к приращению аргумента:

Шаг 4. Вычислим предел этого отношения при , то есть производную:

Геометрический смысл производной

Пусть функция определена на интервале и пусть точка М на графике функции соответствует значению аргумента , а точка Р – значению . Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .

Если существует

проходящую через точку , называют предельным положением секущей МР при (или при ).

Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .

Из определения следует, что для существования касательной достаточно, чтобы существовал предел

,

причём предел равен углу наклона касательной к оси .

Теперь дадим точное определение касательной.

Касательной к графику функции в точке называется прямая, проходящая через точку и имеющая угловой коэффициент , т.е. прямая, уравнение которой

Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x . В этом состоит геометрический смысл производной.